进制&应用

这块一直不是很清楚，在这整理下，以后回来看看；

基础

16 进制

todo

进制转换

let num2 = 69;
// "69" => 6*10^1 + 9*10^0 => 69
num2.toString(2);
// "1000101" => 1*2^6 + 0*2^5 + 0*2^4 + 0*2^3 + 1*2^2 + 0*2^1 + 1*2^0 => 64+4+1 => 69
num2.toString(3);
// "2120" => 2*3^3 + 1*3^2 + 2*3^1 + 0*3^0 => 54+9+6 => 69
num2.toString(4);
// "1011" => 1*4^3 + 0*4^2 + 1*4^1 + 1*4^0 => 64+4+1 => 69
num2.toString(8);
// "105" => 1*8^2 + 0*8^1 + 5*8^0 => 64+4+1 => 69
num2.toString(16);
// "45"=> 4*16^1 + 5*16^0 => 64+5 => 69

存储单位

• bit（比特）,二进制的一位，即 1bit。即 “0” 或者 “1”
• Byte（字节）,1 Byte = 8 bit
• KB（千字节）

1 Bite = 8 bit
1 KB = 1024 B
1 MB = 1024 KB
1 GB = 1024 MB
1 TB = 1024 GB

参考

• bit ( 比特 )和 Byte（字节）的关系？

编码

ASCII 码

• 美国人发明了 ASCII 编码规则, 用一个字节在计算机中表示他们的语言
• ASCII 码常用对照表

GB2312 编码

• 两个字节来表示汉字, 两个字节有 16 位, 有 256*256 种表示方式, 于是可以表示 6W+的字符, 常用的汉字都能表示
• 编码规则 & 编译器

其他国家的编码

• …各国也创建了自己的编码, 于是混乱就开始, 各国之间文本完全不能流通, 因为所用的编码不同

Unicode 编码

• 全球唯一的一套编码, 可容纳全球的所有字符
• 缺点：每个字符使用的字节数一样多, 都用 4 个字节(UCS-4 标准)表示, 比如英文, 只要一个字节就能存储, 但用 Unicode 就需要用 4 个字节, 这是不能接受的.
• 只是一套编码规则的定义

UTF-8 编码

• 只是 Unicode 的一种实现

Base64 编码

• 意义

1. 当不可见字符(部分 ascii)在网络上传输时，由于不同的设备对字符的处理方式有一些不同，这样那些不可见字符就有可能被处理错误，这是不利于传输的。 为了解决这个问题，我们可以先对数据进行编码，比如 base64 编码，变成可见字符，也就是 ASCII 码可表示的可见字符，从而确保数据可靠传输.
2. Base64 的内容是有 0 ～ 9，a ～ z，A ～ Z，+，/ 组成，正好 64 个字符

• 索引表：

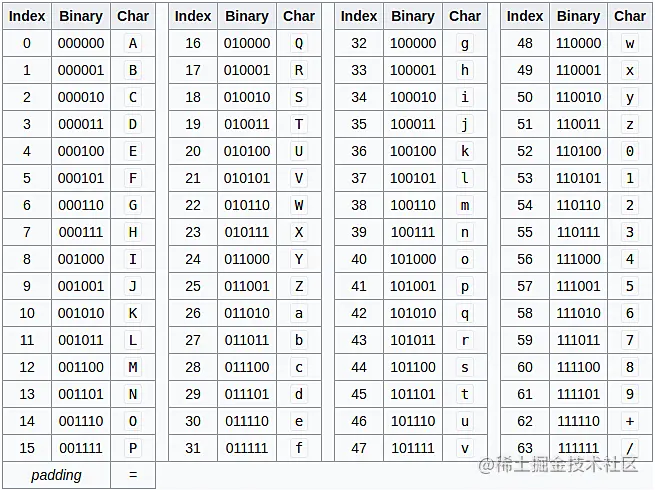
• 案例：’Man’编码过程

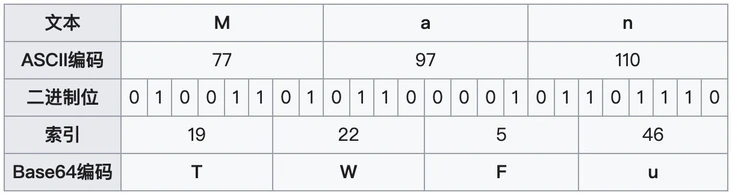
参考

• 字符编码 ASCII, GB2312, Unicode 和 UTF-8 之间的区别
• 字符编码笔记：ASCII，Unicode 和 UTF-8
• [1.3 万字] 玩转前端二进制
• 一文读懂 base64 编码

ECMAPSCRIPT

ArrayBuffer

• 定义

1. 是对固定长度的连续内存区域的引用

2. 不能直接操作其内容，要通过类型数组对象 TypedArray 或 DataView 对象来操作，它们会将缓冲区中的数据表示为特定的格式，并通过这些格式来读写缓冲区的内容

• 语法

new ArrayBuffer(length)，length 单位：字节

TypedArray

所有这些视图（Uint8Array，Uint32Array 等）的通用术语是 TypedArray，用于操作 ArrayBuffer;

let arr = new Uint8Array([0, 1, 2, 3]);
alert(arr.length); // 4，创建了相同长度的二进制数组
alert(arr[1]); // 1，用给定值填充了 4 个字节（无符号 8 位整数）

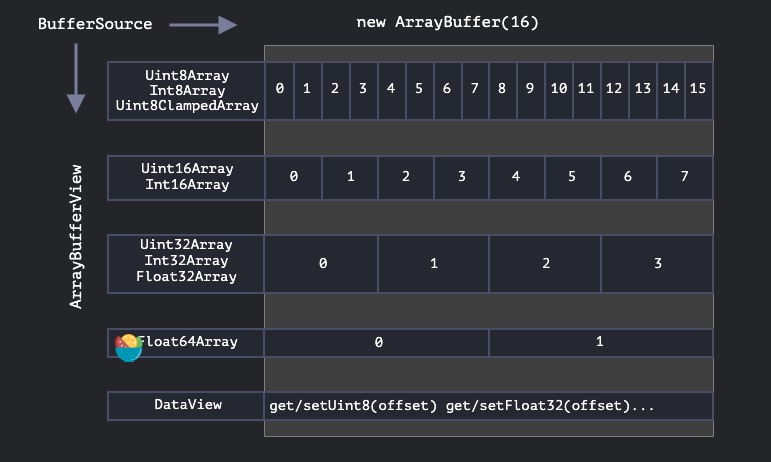
提供很多属性&方法： .buffer、.byteLength、.BYTES_PER_ELEMENT…;.at()、.every()、.fill()、.filter();

参考

• ArrayBuffer，二进制数组
• TypedArray

Web Api

Blob

对象表示一个不可变、原始数据的类文件对象;(The Blob object represents a blob, which is a file-like object of immutable, raw data;)

• 构造

new Blob(blobParts, options);, blobParts 是 Blob/BufferSource/String 类型的值的数组;

• Blob 用作 URL

...
<script>
  let blob = new Blob(["Hello, world!"], { type: "text/plain" });
  link.href = URL.createObjectURL(blob);
</script>

• Blob 转换为 base64

let blob = new Blob(["Hello, world!"], { type: "text/plain" });

let reader = new FileReader();
reader.readAsDataURL(blob); // 将 Blob 转换为 base64 并调用 onload

reader.onload = function () {
  link.href = reader.result; // data url
  link.click();
};

• Image 转换为 blob

let canvas = document.createElement('canvas');
...
canvas.toBlob(function(blob) {
  ...
  link.href = URL.createObjectURL(blob);
}, 'image/png');

• Blob 转换为 ArrayBuffer

blob.arrayBuffer().then(buffer => /* 处理 ArrayBuffer */);

精度问题

单精度&双精度&浮点型

单精度: 1 位符号，8 位指数，23 位小数

双精度: 1 位符号，11 位指数，52 位小数

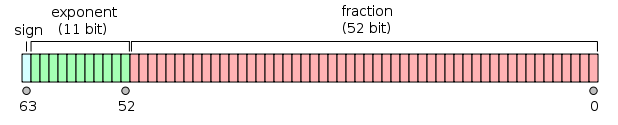
浮点型: 小数点位置可以浮动的数据类型

转换步骤

javascript 以64 位双精度浮点数存储所有 Number 类型值 即计算机最多存储 64 位二进制数(IEEE 754 standard)

例:计算机存储一个 27.5 的数字

• 转换为二进制 11011.1
• 再转换为科学记数法 1.10111*2^4
• 根据 64 位双精度浮点数规则 得到：符号位【0】+指数位【4+1023(固定偏移量)=> 10000000011】+小数部分【10111(52 位不够用 0 补齐)】
• 即0 10000000011 1011 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000

符号位: 1:负数，0:正数; 首位正数1，计算机自行处理，忽略；

经典精度问题

0.1 + 0.2 === 0.30000000000000004

0.1 » 二进制 » 科学记数法 » 实际存储时的形式[64 位] 符号位+(指数位+指数偏移量)+小数部分) 即：

0.1 » 0.0001100110011001100110011001100110011001100110011001101 » 1.100110011001100110011001100110011001100110011001101 * 2^(-4) » 0011111110111001100110011001100110011001100110011001100110011010

同理，0.2 » … » 0011111111001001100110011001100110011001100110011001100110011010;

0.1 >>> 0.0001 1001 1001 1001...（1001无限循环）

0.2 >>> 0.0011 0011 0011 0011...（0011无限循环）

但最多保留 64 位有效数字，需要0 舍 1 入,导致丢失精度

结果如下

0.00011001100110011001100110011001100110011001100110011010 + 0.00110011001100110011001100110011001100110011001100110100 = 0.01001100110011001100110011001100110011001100110011001110

再转为十进制，0.30000000000000004

完整的解决方案

todo（查看下源码）

参考

• 单精度与双精度是什么意思，有什么区别？
• js 精度丢失问题-看这篇文章就够了(通俗易懂)

位运算

Bitwise（操作符）

Operator	usage	desc
按位与	a & b	0101 & 0001 => 0001
按位或	a | b	0101 | 0001 => 0101
按位异	a ^ b	0101 ^ 0001 => 0100; 不相同返回 1
按位非	~ a	~0101 => 1010
左移	a « b	0101 « 1 => 1010
右移	a » b	0101 » 1 => 0010;1101 » 1 => 1110;最左边由符号位补充
无符号右移	a »> b	0101 »> 1 => 0010;1101 »> 1 => 0110;最左边由 0 补充

应用

• 权限设计

p_no = 1
p_a = 1 << 1
p_b = 1 << 2
p_c = 1 << 3
p_d = 1 << 4
add() {
  this.current_p |= permission
},
remP() {
  this.current_p &= ~permission
},
has() {
  return (this.current_p & permission) != 0
}

See the Pen bitwise-auth by 唐鸽 (@tggcs) on CodePen.

参考

• 位运算符